环境光渲染(一)
环境光渲染(一)
1. 定义
使用一张HDR环境图片作为环境光源,每个像素表示一个光源和入射方向,回顾一下渲染方程
显然在实时渲染系统中,针对环境贴图做完整的积分运算代价非常昂贵,所以需要做预处理
2.漫反射部分
2.1 原理
只考虑渲染方程中的漫反射部分
将其中之和光照贴图相关的部分做一个预计算,针对所有球面方向,每个方向做一个半球积分
将结果存成一张新的环境贴图Irradiance,那么最终实时渲染时,漫反射部分可以这个贴图来计算
2.2 漫反射环境贴图的生成
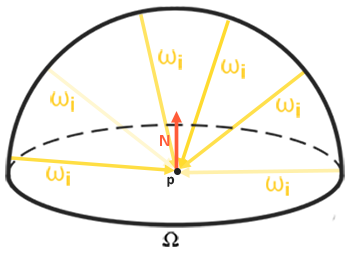
2.2.1 球坐标积分
将立体角转换为球坐标
其中:
代码:
vec3 irradiance = vec3(0.0);
// tangent space calculation from origin point(x'=up, y'=N, z'=left)(left-hand)
vec3 up = vec3(0.0, 1.0, 0.0); //x'
vec3 left = cross(up, N); //z'
up = cross(N, left); //x'
float sampleDelta = 0.025;
float nrSamples = 0.0;
for(float phi = 0.0; phi < 2.0 * PI; phi += sampleDelta)
{
for(float theta = 0.0; theta < 0.5 * PI; theta += sampleDelta)
{
float cosTheta = cos(theta);
float sinTheta = sin(theta);
// spherical to cartesian (in tangent space)
vec3 tangentSample = vec3(cos(phi) * sinTheta, cosTheta, sin(phi) * sinTheta);
// tangent space to world
vec3 sampleVec = tangentSample.x * up + tangentSample.y * N + tangentSample.z * left;
irradiance += texture(environmentMap, sampleVec).rgb * cosTheta * sinTheta;
nrSamples++;
}
}
irradiance = PI * irradiance * float(nrSamples);2.2.2 蒙特卡洛估算
使用蒙特卡洛采样估算积分
其中
方法1:
对于要计算的这个二维积分,如果使用的随机采样是
其中
方法2:
上面的采样方法在极点位置会比较密集,在赤道位置比较稀疏,由于漫反射是均匀分布的,如果采样点也是均匀分布在半球面上的,收敛速度会比较快,这种情况下
其中
vec3 irradiance = vec3(0.0);
vec3 up = vec3(0.0, 1.0, 0.0); //x'
vec3 left = cross(up, N); //z'
up = cross(N, left); //x'
for(uint i=0; i<sampleCounts; i++)
{
//http://holger.dammertz.org/stuff/notes_HammersleyOnHemisphere.html
vec2 uv = Hammersley(i, totalCounts);
// tangent space sample point
float phi = uv.y * 2.0 * PI;
float cosTheta = 1.0 - uv.x;
float sinTheta = sqrt(1-cosTheta*cosTheta);
vec3 tangentSample = vec3(cos(phi) * sinTheta, cosTheta, sin(phi) * sinTheta);
// tangent space to world
vec3 sampleVec = tangentSample.x * up + tangentSample.y * N + tangentSample.z * left;
irradiance += texture2D(s_texSkybox, sampleVec).rgb * cosTheta;
}
irradiance = 2*irradiance / float(sampleCounts);