JPEG算法解密（四）

步骤五：哈弗曼编码

JPEG压缩的最后一步是对数据进行哈弗曼编码(Huffman coding)，哈弗曼几乎是所有压缩算法的基础，它的基本原理是根据数据中元素的使用频率，调整元素的编码长度，以得到更高的压缩比。
举个例子，比如下面这段数据

AABCBABBCDBBDDBAABDBBDABBBBDDEDBD

这段数据里面包含了33个字符，每种字符出现的次数统计如下

字符	A	B	C	D	E
次数	6	15	2	9	1

如果我们用我们常见的定长编码，每个字符都是3个bit。

字符	A	B	C	D	E
编码	001	010	011	100	101

那么这段文字共需要3*33=99个bit来保存，但如果我们根据字符出现的概率来编码，也就是出现频率较高的字符，使用较短的编码，如下：

字符	A	B	C	D	E
编码	110	0	1110	10	1111

那么这段文字共需要3*6+1*15+4*2+2*9+4*1=63个bit来保存，压缩比为63%，哈弗曼编码一般都是使用二叉树来生成的，这样得到的编码符合前缀规则，也就是较短的编码不能够是较长编码的前缀，比如字符'B'使用的编码是'0'，那么其他字符的编码的第一个字符都不能是‘0’。
上面这个编码实例，就是由下面的这颗二叉树生成的。

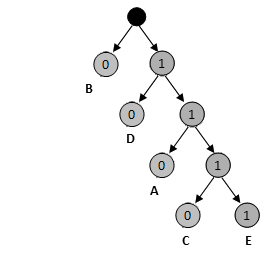
我们回到JPEG压缩上，回顾上一节的内容，经过数据量化，我们现在要处理的数据是一串一维数组，举例如下：

①原始数据

在实际的压缩过程中，数据中的0出现的概率非常高，所以首先要做的事情，是使用RLE编码对其中的0进行处理，把数据中的非零的数据，以及数据前面0的个数作为一个处理单元。

①原始数据
②RLE编码	35	7	0,0,0,-6	-2	0,0,-9	0,0,…,0,8	0,0,…,0

如果其中某个单元的0的个数超过16，则需要分成每16个一组，如果最后一个单元全都是0，则使用特殊字符“EOB”表示，EOB意思就是“后面的数据全都是0”,

①原始数据
②RLE编码	35	7	0,0,0,-6	-2	0,0,-9	0,0,…,0,8		0,0,…,0
	35	7	0,0,0,-6	-2	0,0,-9	0,0,…,0	0,0,8	0,0,…,0
	(0,35)	(0,7)	(3,-6)	(0,-2)	(2,-9)	(15,0)	(2,8)	EOB

其中（15,0）表示15+1也就是16个0，接下来我们要处理的是括号里右面的数字，这个数字的取值范围在-2047~2047之间，JPEG提供了一张标准的码表用于对这些数字编码：

Value		Size	Bits
0		0	–
-1	1	1	0	1
-3,-2	2,3	2	00,01	10,11
-7,-6,-5,-4	4,5,6,7	3	000,001,010,011	100,101,110,111
-15,…,-8	8,…,15	4	0000,…,0111	1000,…,1111
-31,…,-16	16,…,31	5	0 0000,…,0 1111	1 0000,…,1 1111
-63,…,-32	32,…,63	6	00 0000,…	…,11 1111
-127,…,-64	64,…,127	7	000 0000,…	…,111 1111
-255,…,-128	128,…,255	8	0000 0000,…	…,1111 1111
-511,…,-256	256,…,511	9	0 0000 0000,…	…,1 1111 1111
-1023,…,-512	512,…,1023	10	00 0000 0000,…	…,11 1111 1111
-2047,…,-1024	1024,…,2047	11	000 0000 0000,…	…,111 1111 1111

举例来说，第一个单元中的“35”这个数字，在表中的位置是长度为6的那组，所对应的bit码是“100011”，而“-6”的编码是”001″，由于这种编码附带长度信息，所以我们的数据变成了如下的格式。

①原始数据
②RLE编码	35	7	0,0,0,-6	-2	0,0,-9	0,0,…,0,8		0,0,…,0
	35	7	0,0,0,-6	-2	0,0,-9	0,0,…,0	0,0,8	0,0,…,0
	(0,35)	(0,7)	(3,-6)	(0,-2)	(2,-9)	(15,0)	(2,8)	EOB
③BIT编码	(0,6, 100011)	(0,3, 111)	(3,3, 001)	(0,2, 01)	(2,4, 0110)	(15,-)	(2,4, 1000)	EOB

括号中前两个数字分都在0~15之间，所以这两个数可以合并成一个byte，高四位是前面0的个数，后四位是后面数字的位数。

①原始数据
②RLE编码	35	7	0,0,0,-6	-2	0,0,-9	0,0,…,0,8		0,0,…,0
	35	7	0,0,0,-6	-2	0,0,-9	0,0,…,0	0,0,8	0,0,…,0
	(0,35)	(0,7)	(3,-6)	(0,-2)	(2,-9)	(15,0)	(2,8)	EOB
③BIT编码	(0,6, 100011)	(0,3, 111)	(3,3, 001)	(0,2, 01)	(2,4, 0110)	(15,-)	(2,4, 1000)	EOB
③BIT编码	(0x6,100011)	(0x3,111)	(0x33,001)	(0x2,01)	(0x24,0110)	(0xF0,-)	(0x24,1000)	EOB

对于括号前面的数字的编码，就要使用到我们提到的哈弗曼编码了，比如下面这张表，就是一张针对数据中的第一个单元，也就是直流(DC)部分的哈弗曼表，由于直流部分没有前置的0，所以取值范围在0~15之间。

Length	Value	Bits
3 bits	04 05 03 02 06 01 00 (EOB)	000 001 010 011 100 101 110
4 bits	07	1110
5 bits	08	1111 0
6 bits	09	1111 10
7 bits	0A	1111 110
8 bits	0B	1111 1110

举例来说，示例中的DC部分的数据是0x06，对应的二进制编码是“100”，而对于后面的交流部分，取值范围在0~255之间，所以对应的哈弗曼表会更大一些

Length	Value	Bits
2 bits	01 02	00 01
3 bits	03	100
4 bits	00 (EOB) 04 11	1010 1011 1100
5 bits	05 12 21	1101 0 1101 1 1110 0
6 bits	31 41	1110 10 1110 11
…	…	…
12 bits	24 33 62 72	1111 1111 0100 1111 1111 0101 1111 1111 0110 1111 1111 0111
15 bits	82	1111 1111 1000 000
16 bits	09 … FA	1111 1111 1000 0010 … 1111 1111 1111 1110

这样经过哈弗曼编码，并且序列化后，最终数据成为如下形式

①原始数据
②RLE编码	35		7		0,0,0,-6		-2		0,0,-9		0,0,…,0,8			0,0,…,0
	35		7		0,0,0,-6		-2		0,0,-9		0,0,…,0	0,0,8		0,0,…,0
	(0,35)		(0,7)		(3,-6)		(0,-2)		(2,-9)		(15,0)	(2,8)		EOB
③BIT编码	(0,6, 100011)		(0,3, 111)		(3,3, 001)		(0,2, 01)		(2,4, 0110)		(15,-)	(2,4, 1000)		EOB
③BIT编码	(0x6,100011)		(0x3,111)		(0x33,001)		(0x2,01)		(0x24,0110)		0xF0	(0x24,1000)		EOB
④哈弗曼编码	100	100011	100	111	1111 1111 0101	001	01	01	1111 1111 0100	0110	1111 1111 001	1111 1111 0100	1000	1010
⑤序列化
⑤序列化