TheCodeWay:我的博客

这是我以前写的一篇博文，因为有朋友需要，重新贴出来

        一个程序里用到了计算线段和圆相交情况的算法，在这里记下来备忘

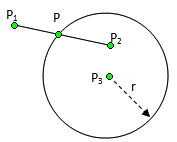
        设线段的两个端点分别是P1(x1,y1)和P2(x2,y2)，圆的圆心在P3(x3,y3)，半径为r，那么如果有交点P(x,y)的话
\begin{equation}
\overrightarrow{P}=\vec{P_1}+u(\vec{P_2}-\vec{P_1})\tag1
\end{equation}
        其中，u在0到1之间，转换成各个坐标
\begin{equation}
\begin{cases}
x=&x_1+u(x_2-x_1)\\
y=&y_1+u(y_2-y_1)
\end{cases}\tag2
\end{equation}
        由于P也在圆上，所以
\begin{equation}
(x-x_3)^2+(y-y_3)^2=r^2\tag3
\end{equation}
        联立上面的公式，可以得到
\begin{equation}
Au^2+Bu+C=0\tag4
\end{equation}
        其中
\begin{equation}
\begin{cases}
A=&(x_2-x_1)^2+(y_2-y_1)^2\\
B=&2((x_2-x_1)(x_1-x_3)+(y_2-y_1)(y_1-y_3))\\
C=&x_3^2+y_3^2+x_1^2+y_1^2-2(x_3x_1+y_3y_1)-r^2
\end{cases}\tag5
\end{equation}
        解一元二次方程，可以得到
\begin{equation}
u=\frac{-B\pm\sqrt{B^2-4AC}}{2A}\tag6
\end{equation}
        根据B²-4AC的结果，可以判断线段所在直线和圆的相交情况

• 如果小于0，表示没有交点
• 如果等于0，表示相切，只有一个交点
• 如果大于0，表示有两个交点

        针对P1和P2之间的线段，根据计算出的u值，有5种结果

• 如果线段和圆没有交点，而且都在圆的外面的话，则u的两个解都是小于0或者大于1的
• 如果线段和圆没有交点，而且都在圆的里面的话，u的两个解符号相反，一个小于0，一个大于1
• 如果线段和圆只有一个交点，则u值中有一个是在0和1之间，另一个不是
• 如果线段和圆有两个交点，则u值得两个解都在0和1之间
• 如果线段和圆相切，则u值只有1个解，且在0和1之间