今天起,正式不惑了
从抛币协议到智能合约(二)
除了抛币协议,加密领域还有一个很有趣的课题和游戏的去中心化直接相关,就是Mental Poker协议,中文一般翻译成“智力扑克”,但我认为这个翻译并不准确,“Mental Poker”一词来源于1979年的一篇论文《Mental Poker》,作者是Shamir,Rivest和Adleman(就是发明RSA算法的三位大牛),里面这么描述这个场景:

Mental这个词在这里应该是意念或者思维的意思,和盲棋是对应的,但中文中并没有“意念扑克”这样的词,所以翻译成“盲牌协议”其实更贴切一些。和象棋围棋这样的信息公开游戏不同,扑克游戏大部分都有发牌环节,玩家手中的牌是保密的,所以两位象棋大师完全可以在电话里通过“炮二平五、马八进七”来一局象棋,但扑克牌就不行了,你说手里有一对Ace,我怎么知道你没撒谎呢?
所以Mental Poker协议最关键的就是洗牌和发牌这个流程,这个过程既要保证是随机和公平的,又要保证玩家的手牌的私密性,在这篇论文里给了一个巧妙的方法,先举个形象的例子:
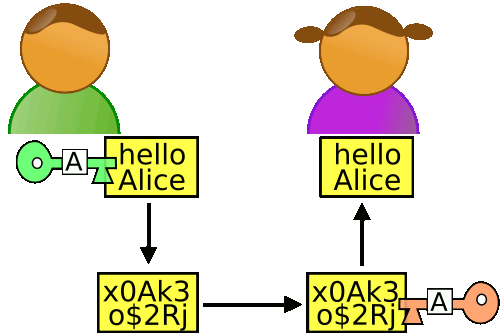
Alice想把一件珍宝通过信使送给Bob,但信使非常不可靠,没有锁进箱子的东西他一定会偷的,并且如果让信使拿到钥匙他也一定会去打开锁的,那在这种情况下Alice和Bob有什么办法安全的把宝物送给对方呢?答案是:Alice用箱子把宝物装进去,然后用自己的锁把箱子锁起来送给Bob,Bob收到箱子后再加上一把自己的锁,把箱子再送回给Alice,Alice收到后打开自己的锁送回给Bob,最后Bob收到箱子之后再打开自己的所,就可以拿到宝物了。
按这个思路换成扑克牌游戏,假设Alice和Bob要玩一局扑克牌游戏,开局的时候他们都要一副牌(52张)中各抽取5张,那么过程就是这样: Continue reading “从抛币协议到智能合约(二)”
从抛币协议到智能合约(一)
最近区块链非常火,也有人在讨论游戏和区块链的结合,就目前来看,已有的区块链游戏无非就是两种,一种就是类似于CryptoKitties这样的虚拟资产游戏,还有就是博彩类的游戏,比如中本聪筛子,vDice等。

这是我当初花了300刀买的一只CryptoKitties,编号448412
严格来说,这些都不算是真正的游戏,在我看来,区块链游戏起码要做到真正的去中心化,能够实现玩家和玩家之间的互动,并且能提供玩家最基本的游戏乐趣才行。而目前所谓的区块链游戏还远远无法满足这几点,而且现在的区块链被笼罩在非常不好的资本炒作氛围中,所谓的区块链创业大部分都是挂羊头卖狗肉而已。
从技术上讲,游戏的去中心化并不是一件新鲜事,比如加密领域的“抛币协议”可以算是这方面的老祖宗了。早在1981年,数学家Manuel Blum就曾经发表了一篇著名的论文《Coin Flipping by Telephone: A Protocol for Solving Impossible Problems.》,在开篇就提出一个有趣的情景:

简单的描述就是两个人想通过抛硬币来决定解决他们之间的分歧,那么如何通过电话或者互联网来实现这个行为呢?很显然让其中一个人来随机是不行的,因为他们互不信任,两个人合作呢?比如说双方各自从0和1之间随机一个值,然后把两个值异或作为最终的结果?也不行,比如说Alice随机出0或者1,她把这个数告诉Bob,那么Bob就有机会根据Alice随机到的值操纵最后结果。所以想得到真正公平的结果,抛币协议必须能够满足“抛币入井”的特性,如同把硬币扔进井中,双方只可以去观看而不能改变结果。
一种简单的方法是利用单向函数,比如首先让Alice准备一个随机字符串,其中包含”head”或者”tail”作为抛币结果, 然后把这个字符串的hash值给Bob,让Bob猜是head还是tail,最后Alice把原始的字符串公布以验证。这个协议利用了hash函数是单向函数的特性,由于Bob只收到了hash值,他无法判断原始字符串,所以无法作弊,而Alice如果想抵赖,就需要能够操纵这个hash函数,重新构造出一个字符串使其hash值和发给Bob的那个一摸一样,这也是不可能的(或者说很困难的),在WikiPedia给出了一种这个协议的具体实现。
 但Blum给出的协议并不是这样,原因是使用hash函数并不“严肃”,因为很难对其进行严格的安全性分析,尽管Bob无法从hash值反推回原来的字符串,但他很可能发现一些蛛丝马迹,而且靠其中一方直接随机出抛币结果也不公平,因为这需要依赖很高质量且双方都信任的随机函数,Blum的抛币协议可以简单的描述为下面的过程:
但Blum给出的协议并不是这样,原因是使用hash函数并不“严肃”,因为很难对其进行严格的安全性分析,尽管Bob无法从hash值反推回原来的字符串,但他很可能发现一些蛛丝马迹,而且靠其中一方直接随机出抛币结果也不公平,因为这需要依赖很高质量且双方都信任的随机函数,Blum的抛币协议可以简单的描述为下面的过程:
1. 首先Bob准备一个Blum整数\(n=pq\),并且把\(n\)发送给Alice
2. Alice随机一个小于\(n\)且和\(n\)互质的数\(x\),计算\(y=x^2 \mod n\),然后把\(y\)发送给Bob
3. Bob猜\(x\)的雅可比符号\((x\mid n)\)是1还是-1,并且把猜测的结果发送给Alice
4. Alice向Bob出示\(x\)
5. Bob且向Alice出示\(p,q\)
6. 双方根据Bob是否猜对来决定硬币是正面还是反面,并且检测对方在这个过程中有没有作弊。
这个协议利了数论中的一些基本知识,因为并不算复杂,这里先简单介绍一下:
二次剩余(Quadratic residue)
对于整数\(n\)和\(q\),如果存在整数\(x\)满足\(x^2\equiv q\pmod{n}\),那么就称\(q\)是\(n\)的二次剩余
比如2就是7的一个二次剩余,因为\(3^2\equiv2\pmod7\),但5就不是7的二次剩余,因为找不到一个数满足\(x^2\equiv5\pmod7\),这种情况称5是7的二次非剩余。 Continue reading “从抛币协议到智能合约(一)”
转载:RSA算法原理(二)
原文链接: http://www.ruanyifeng.com/blog/2013/07/rsa_algorithm_part_two.html
作者: 阮一峰
日期: 2013年7月 4日
上一次,我介绍了一些数论知识。
有了这些知识,我们就可以看懂RSA算法。这是目前地球上最重要的加密算法。

六、密钥生成的步骤
我们通过一个例子,来理解RSA算法。假设爱丽丝要与鲍勃进行加密通信,她该怎么生成公钥和私钥呢?
第一步,随机选择两个不相等的质数p和q。
爱丽丝选择了61和53。(实际应用中,这两个质数越大,就越难破解。)
第二步,计算p和q的乘积n。
爱丽丝就把61和53相乘。
\begin{equation}n = 61×53 = 3233\end{equation}
n的长度就是密钥长度。3233写成二进制是110010100001,一共有12位,所以这个密钥就是12位。实际应用中,RSA密钥一般是1024位,重要场合则为2048位。 Continue reading “转载:RSA算法原理(二)”
转载:RSA算法原理(一)
最近再看加密算法的时候本来想写一篇关于RSA算法的,后来发现阮一峰写的这篇文章实在是太好了,就直接转载到这里了
原文链接:http://www.ruanyifeng.com/blog/2013/06/rsa_algorithm_part_one.html
作者: 阮一峰
日期: 2013年6月27日
如果你问我,哪一种算法最重要?
我可能会回答”公钥加密算法“。

因为它是计算机通信安全的基石,保证了加密数据不会被破解。你可以想象一下,信用卡交易被破解的后果。
进入正题之前,我先简单介绍一下,什么是”公钥加密算法”。
一、一点历史
1976年以前,所有的加密方法都是同一种模式:
(1)甲方选择某一种加密规则,对信息进行加密;
(2)乙方使用同一种规则,对信息进行解密
由于加密和解密使用同样规则(简称”密钥”),这被称为”对称加密算法“(Symmetric-key algorithm)。
这种加密模式有一个最大弱点:甲方必须把加密规则告诉乙方,否则无法解密。保存和传递密钥,就成了最头疼的问题。

1976年,两位美国计算机学家Whitfield Diffie 和 Martin Hellman,提出了一种崭新构思,可以在不直接传递密钥的情况下,完成解密。这被称为”Diffie-Hellman密钥交换算法“。这个算法启发了其他科学家。人们认识到,加密和解密可以使用不同的规则,只要这两种规则之间存在某种对应关系即可,这样就避免了直接传递密钥。
这种新的加密模式被称为”非对称加密算法”。
(1)乙方生成两把密钥(公钥和私钥)。公钥是公开的,任何人都可以获得,私钥则是保密的。
(2)甲方获取乙方的公钥,然后用它对信息加密。
(3)乙方得到加密后的信息,用私钥解密。
如果公钥加密的信息只有私钥解得开,那么只要私钥不泄漏,通信就是安全的。 Continue reading “转载:RSA算法原理(一)”
跨平台网络库Cyclone发布
我在畅游工作时,曾经维护一个名为Cyclone的基础库,包括天龙八部在内的大部分端游产品都是使用的这个库,主要是网络通讯、消息包管理,加密等功能,但这个库本身的技术含量很低,网络部分只支持select,没有考虑多线程,代码也很丑陋。由于是关系现金流的核心产品,本着稳定压倒一切的原则,一直不敢动,所以至今畅游仍然还在用着这份十多年前的代码。2015年初的时候,我曾经有一段时间没什么事情,于是打算重新写一个全新的网络库,参考了Nginx、Skynet、Muduo、lwan、libevent的设计之后,有了一些心得,于是开始写新版的cyclone。在离开畅游之前,cyclone已经完成了第一版,并且应用在一个在研的手游项目上,但这个版本并不完善,后来我一直想找时间把cyclone再完善一下,但对于创业狗来说,坐下来写代码简直就是大逆不道的事情,于是一直断断续续的写。直到最近,cyclone终于完成一个比较满意的版本,也算完成了一个心愿 🙂

这个工程我放在了Github上,cyclone的设计从一开始就是比较清晰的,主要是以下几个特性
非阻塞+多路复用
这应该是使用最为广泛的一种网络模型,适合大多数应用场景,multiplexing支持select、epoll、kqueue三种api
多线程+event loop机制
cyclone是按照one loop per thread的思想设计的,线程通过event唤醒,线程之间的通讯通过pipe进行,这种模式可以最大程度上减少线程的空转以及线程之间的临界区。对于网游服务器来说,一种很不好的设计就是不考虑线程的空转成本,大量使用sleep+busy loop,这也是为什么很多情况下,一台网游服务器明明cpu占用很低,但玩家仍然觉得“卡”的原因,因为大量的空转逻辑,导致服务器线程的fps降低,对玩家的消息包的相应时间加长导致的。线程之间的通讯使用无锁队列+pipe机制,也就是把要传输的数据放在无锁队列中,然后通过pipe唤醒相应的目标线程。对于c++多线程程序来说,对象的生命周期管理是一个非常重要的问题,一不小心就会陷入泥潭,所以采用线程之间的消息通讯机制,再配合std::shared_ptr,可以大大降低问题的复杂度。
跨平台
目前支持Windows、Linux、MacOSX、Android,后面会考虑支持iOS,因为用了很多c++11特性,所以跨平台并不是什么太麻烦的事情,主要的跨平台的差异还是在于EventLoop中针对不同平台的实现,cyclone的EventLoop支持socket,timer,pipe三种唤醒机制,其中pipe的实现在linux和mac上都有原生的支持,在windows上虽然也有pipe,但无法用在select上,所以我用了一对socket来模拟pipe,这个消耗会有些高,所以在windows的生产环境里尽量慎用pipe。timer在mac上使用了kqueue原生机制,linux和Android使用了timerfd,windows上使用了timer-queue + pipe的方式。
cyclone使用CMake作为编译脚本,以及单元测试程序,如果需要编译单元测试的话,需要安装google test
工具函数
cyclone的设计思想是宁缺毋滥,尽量保证库的简单,比如消息包的封装,加解密这样的代码是以工具的形式放在库里,我已经把dh-exchange密钥交换和aes加密放在库里,可以实现通讯双方的安全协议,另外adler32可以做简单的crc校验算法,xorshift128做异或加密。
范例
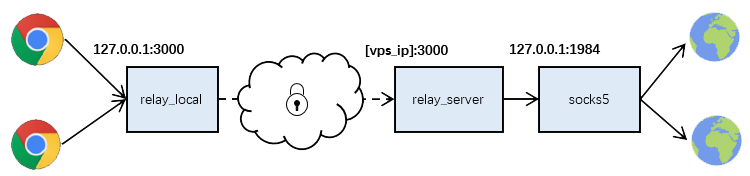
我提供了几个类似于helloworld的范例,比如echo和chat,另外samples里还有两个很有用的程序,socks5和relay。把这两个程序写出来的目的其实大家都懂得,socks5这个程序实现了简单的Socks5协议代理服务器,配合海外的vps,可以实现科学上网,但在我大天朝,仅仅靠sockes5还不行,因为这个协议本身并不支持消息加密,很容易就会莫名其妙的挂掉,所以我又实现了加密用的relay。原理可以参照云风的这篇文章。其中relay_local是一个n:1的工具,把多个链接收到一个链接中,relay_server是1:n的工具,把链接恢复出来去和真正的目标程序通讯,而relay_local和relay_server之间的协议是通过密钥交换和aes算法加密的,所以非常安全。
具体操作是,在海外的vps上,运行socks5和relay_server,如下:
|
1 2 |
./socks5 -p 1984 ./relay_server -uh 127.0.0.1 -up 1984 -p 3000 |
在本地机器上运行relay_local
|
1 |
./relay_local -uh [VPS_IP] -up 3000 -p 1984 |
完全使用HTTPS了
以前用过CloudFlare免费SSL证书来实现这个网站的https访问,不过CloudFlare是利用dns解析,把浏览器和服务器之间的数据通过中间服务器加密来实现,速度很慢而且只能使用固定的dns,所以不久我就把这个功能关掉了。最近偶然发现了一家可以提供免费SSL证书的机构Let’s Encrypt

简单了解了一下,Let’s Encrypt是国外一个公共的免费SSL项目,由 Linux 基金会托管,它的来头不小,由Mozilla、思科、Akamai、IdenTrust和EFF等组织发起,目的就是向网站自动签发和管理免费证书,以便加速互联网由HTTP过渡到HTTPS,目前Facebook等大公司开始加入赞助行列。目前Let’s Encrypt的证书已经被Mozilla、Google、Microsoft和Apple等主流的浏览器所信任,所以使用起来完全没有问题。证书的申请也很简单,官方有一套自动化的脚本(https://github.com/certbot/certbot)可以完成所有工作
首先把脚本clone到本地
|
1 2 3 |
git clone https://github.com/certbot/certbot cd certbot chmod +x ./certbot-auto |
生成证书(注意,生成证书时,需要临时关闭nginx服务)
|
1 |
./certbot-auto certonly --standalone --email thejinchao@gmail.com -d thecodeway.com -d www.thecodeway.com |
生成的证书放在/etc/letsencrypt/live/目录下,可以通过tree命令查看
|
1 |
tree /etc/letsencrypt/live/ |
在nginx的配置文件中加入ssl服务器定义
|
1 2 3 4 5 6 7 8 9 10 |
server { listen 443; server_name www.thecodeway.com thecodeway.com; #... ssl on; ssl_certificate /etc/letsencrypt/live/thecodeway.com/fullchain.pem; ssl_certificate_key /etc/letsencrypt/live/thecodeway.com/privkey.pem; ssl_protocols TLSv1 TLSv1.1 TLSv1.2; #... } |
再把原先的http部分重定向到https
|
1 2 3 4 5 |
server { listen 80; server_name www.thecodeway.com thecodeway.com; return 301 https://$server_name$request_uri; } |
重新启动服务器之后,即可看到所有链接已经变成绿色的https链接了。需要注意的是,Let’s Encrypt的证书的有效期只有三个月,所以需要设置一个定时任务,定期更新证书
|
1 |
./certbot-auto renew --standalone --pre-hook "service nginx stop" --post-hook "service nginx start" --force-renewal |
另外推荐一个检测网站ssl链接安全性的网站:https://www.ssllabs.com/ssltest/index.html
在UnrealEngine4中使用Google Protobuf
最近项目中需要把Google protobuf加入到UnrealEngine4游戏工程中,积累下一些有用的经验分享下。
UE有一套自己的编译规则,如何在游戏中添加第三方库官方有一篇很详细的文档(Linking Static Libraries Using The Build System)。
简单来说,第三方库一般放在’Source/ThirdParty’目录下,建一个目录,把需要包含的头文件以及编译好的库都放在这里,然后写一个对应的[LIBNAME].Build.cs文件,在这个文件里需要告诉编译器需要修改的设置,例如添加那些包含目录以及链接库。在游戏工程使用时,需要在本工程文件的[APPNAME].Build.cs中添加对该库的引用,就像下面这样
|
1 2 |
PublicDependencyModuleNames.AddRange(new string[] { "Core", "CoreUObject", "Engine", "InputCore", "HeadMountedDisplay", "libprotobuf" }); |
对第三方库的使用,可以参照UnrealEngine的源码,在它的源码目录’Source/ThirdParty’里,有一大堆第三方库,不过这些库都是预先编译好的.lib和.a,如何编译出这些库官方并没有提供详细的文档说明。对于Windows环境来说比较简单,首先是使用和UE编辑器同样的VisualStudio版本,例如目前最新的4.14使用的是VS2015,并且在编译中使用/MD选项。google protobuf本身提供了一套cmake编译脚本,可以很方便的编译出所需要的lib文件。
比较麻烦的是Linux平台,UE提供了专门的clang工具链来作为Linux和Android平台的编译工具,可以参照官方的这篇文档下载安装(Compiling For Linux),不过这套工具链中并没有对应的make工具,所以我从UE源码中的UnrealBuildTool工具中把编译参数还原出来,手动写了一套python脚本来完成probobuf的编译。
为了适应UE4的环境,需要做一些改动,首先是protobuf中使用了类似于UINT这样的数据类型,而这种数据类型在UE4的源码中已经被屏蔽,具体可以参考UE源码中DisableOldUETypes.h文件的说明,为了使两者兼容,需要在protoc产生的.pb.h文件中添加#include “AllowWindowsPlatformTypes.h”和#include “HideWindowsPlatformTypes.h”两行代码。
|
1 2 3 4 5 6 7 8 9 |
#ifdef _MSC_VER #include "AllowWindowsPlatformTypes.h" #endif //include other header file #ifdef _MSC_VER #include "HideWindowsPlatformTypes.h" #endif |
另外protobuf源码中有一个文件使用了byteswap.h这个头文件,不幸的是,UE4源码中有一个ByteSwap.h文件,在clang编译器中产生编译错误,需要做一定的修改。
|
1 2 3 4 5 6 |
//google/protobuf/stubs/port.h, line 91 //#include <byteswap.h> // IWYU pragma: export #include <bits/byteswap.h> #define bswap_16(x) __bswap_16 (x) #define bswap_32(x) __bswap_32 (x) #define bswap_64(x) __bswap_64 (x) |
我把最终编译好的库以及所使用的的编译脚本放到了github上,所需环境如下
| 软件 | 版本 | 备注 |
|---|---|---|
| Google Protobuf | 3.1.0 | |
| Visual Studio | 2015 | |
| clang | 3.9.0 | EPIC提供改造过的工具链,需要参照这篇官方文档下载安装 |
| CMake | 2.8以上 | 需要把cmake.exe所在路径加入到PATH路径中 |
| Unreal Engine Source | 4.14.3 | 参照官方文档下载并编译源码 |
| Python | 3.x or 2.x |
星辰大海
赌博中的数学:Martingle策略
前段时间在Las Vegas待了一个星期左右,以前虽然也来过赌城,但不像这次这么长时间,趁机好好体验了一把赌徒的生活。

来赌场的华人最爱玩的是一种叫做“百家乐”(Baccarat)的游戏,这个游戏的规则并不复杂,节奏也很快,简单来说,就是类似于最简单的猜大小的游戏,每局产生的结果有三种可能性,要么是“庄”,要么是“闲”,或者是“和”,每个结果的概率和赔率大概分布如下:
| 结果 | 概率 | 赔率 |
|---|---|---|
| 庄 | 45.86% | 0.95 |
| 闲 | 44.62% | 1 |
| 和 | 9.52% | 8 |
举个例子,假如押10块钱到“庄”上,如果牌局结果是“庄”,那么不仅可以把本金10块拿回来,还可以再获得9.5元,但如果结果是“闲”,那么这10块钱本金就赔进去了。很多赌徒之所以痴迷百家乐,除了节奏明快,百家乐的发牌方式设计的也很独特,先发两张牌,然后再通过一定的规则“补牌”,在补牌的过程中结果可能完全反转,整个过程很“刺激”,另外一个原因来自于百家乐的“路单”。所谓路单就是用来记录赌局已经产生的结果的图案,除了直接记录每一局是“庄”、“闲”还是“和”,百家乐的路单中还有“大路”、“大眼仔”、“小路”、“曱甴路”这些古怪的额外数据,用来记录诸如结果是否“齐整”等信息。
作为一个死理性派,我自然一开始就明白“赌徒谬论”(Gambler’s fallacy)这个道理,所有赌局在概率上都是互相独立的,即便连续开出十几次“庄”,下一次是庄的概率仍然是45.86%,那些花花绿绿的路单纯粹就是给人心理安慰罢了,所以我始终没有去费力气分析什么路单,但我一直在尝试另一个和赌博相关的问题,就是“Martingle策略”(Martingale)。
Maringle是一种投资策略,在赌徒中间流传甚广,这种策略可以简单描述为“输钱后加倍下注,直到赢钱”。比如在百家乐游戏中,我一开始押10元到“闲”上,如果押对,那么下次仍然继续押10元,如果押错,相当于我赔掉了10元,那么第二局就押20元,这样如果第二局赢得话,我就可以获得40元,刨除两局投入的30元,仍然盈利10元,如果继续输,那么就加倍到40、80、160…元,这样一旦赢钱,就可以把连续输掉的钱都翻本回来。

理论上讲,如果本金足够,并且赌局没有押注上限的话,这种方法是可以绝对盈利的,事实上也的确如此,Martingle策略最早在18世纪就在法国的赌场上流行,我在拉斯维加斯用这个策略,用5美金做最小赌注押“闲”,一度把1000美元本金翻到3000美元,当时心情激动,认为找到了发财的好方法。不过好景不长,很快我遇到连续的“庄”,几乎在瞬间,我几天辛辛苦苦赢来的钱就全赔了进去,最终兴趣索然,就再也不玩了。
为了真实重现这种状况,我用Mathematic模拟了一下Martingle策略:
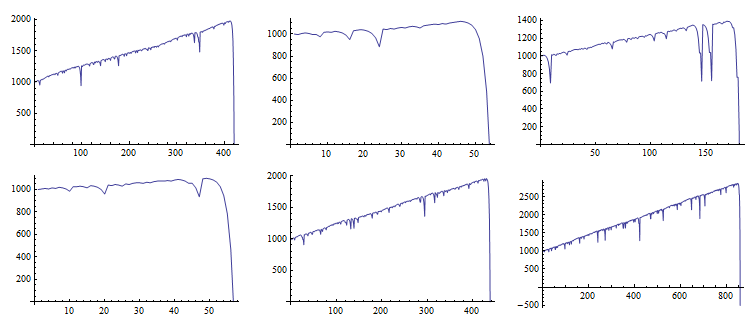
其实这就是Martingle策略的真相,在运气比较好的情况下,通过输和赢交替进行,资产会小量的逐渐提升,不过一旦遇到连续输的结果,押注翻倍上升,而获利仍然是最小押注,风险就会急剧升高,最终无一例外出现破产出局的情况,所以使用这种策略的最终要的事情就是“见好就收”,一旦赢到一定程度就赶紧收手,所谓久赌必输就是这个道理。